TD/TP - Parcours séquentiel

Exercice

Extrait de NSI prépabac première générale

On veut écrire une fonction qui permet de calculer la moyenne des notes en tenant compte de leur coefficients.

On propose le code suivant:

def moyenne_ponderee(lst_notes, lst_coefs):
    """lst_notes et lst_coefs sont deux tableaux de nombres.
    Renvoie la moyenne pondérée des notes (float)
    """
    somme_pond = 0
    somme_coefs = 0
    # LA
    for i un range(len(lst_note)):
        somme_pond = somme_pond + lst_notes[i] * lst_coefs[i]
        somme_coefs = somme_coefs + lst_coefs[i]
        # ICI
    return somme_pond / somme_coefs

On utilise la fonction ainsi:
```
notes = [12, 5, 9, 23]
coefficients = [3, 2, 5, 1]
print(moyenne_ponderee(notes,coefficients))
```
Compléter le tableau avec les valeurs des expressions à chaque passage par la ligne indiquée (LA et ICI).

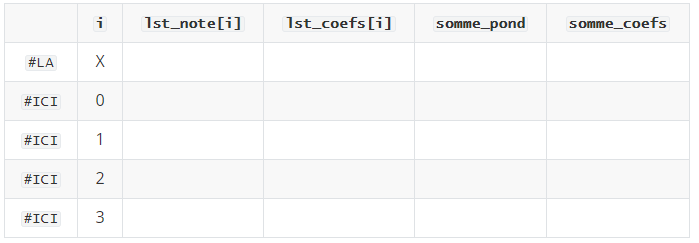
Que se passe-t-il lors de l’exécution du code suivant?

notes = [12, 5, 9, 23]
coefficients = [3, 2, 5, 1, 7]
print(moyenne_ponderee(notes,coefficients))

Que se passe-t-il lors de l’exécution du code suivant?
```
notes = [12, 5, 9, 23]
coefficients = [3, 2, 5 ]
print(moyenne_ponderee(notes,coefficients))
```
Exercice
1. À l’aide d’un des exemples du cours compléter la fonction qui prend en entrée un tableau de nombres et un nombre et renvoie l’indice de la première fois qu’est rencontré ce nombre et si ce nombre n’est pas dans le tableau.
```
def recherche_seq(tab,elem):
    for i in range(len(tab)):
        if tab[i] == elem:
            return ...
    return ...

assert recherche_seq([2,4,6,1],1)== 3
assert recherche_seq([7,4,2,9,8],4)==1
assert recherche_seq([7,4,2,9,8],3)==None
```
2. Créer un fichier tp_seq.py dans lequel vous testerez le programme de la première question.
Exercice

Écrire une fonction qui prend en entrée une chaîne de caractères et un caractère et qui renvoie le nombre de fois que ce caractères apparaît dans la chaîne (sans utiliser la méthode ). Par exemple:
```
>>> frequence("Bonjour tout le monde","o")
4
>>> frequence("Salut !!","o")
0
```
Écrire dans votre fichier tp_seq.py une fonction qui prend en entrée un tableau de nombres et renvoie le produit de ces nombres.

Par exemple:
```
>>> produit([1,2,3)
6
>>> produit([3,4,5,2])
120
```
Exercice
1. Écrire dans votre fichier tp_seq.py une fonction qui prend en entrée un tableau de nombres et renvoie le plus petit des nombres de ce tableau. Mettre quelques pour tester votre fonction.
2. Écrire une fonction qui prend en entrée un entier strictement positif et renvoie un tableau de taille contenant des nombres entiers aléatoires compris entre 1 et .
3. chercher sur Internet la description de la fonction du module
4. Vous trouverez ci-dessous le programme qui a créé le graphique du premier exemple du cours. En vous aidant de programme, faire un programme dans un fichier nommé tp_seq_min.py qui test le temps d’exécution de votre fonction pour des tableaux de tailles 50,100,200,400,800 et 1600. Attention il est normal que ce programme prenne plusieurs minutes à être exécuté. Tant que vous n’êtes pas certain de votre programme utiliser tester le temps pour tes tableaux de taille 50 et 100 uniquement afin de ne pas avoir à attendre trop longtemps.
5. D’après votre graphique, votre fonction est-elle bien linéaire? C’est-à-dire est-ce que le temps d’exécution est proportionnel à la longueur du tableau?
```
from timeit import timeit
import matplotlib.pyplot as plt
#Code de la fonction à tester
code ="""
def recherche(tab,elem):
    for e in tab:
        if e == elem:
            return True
    return False
recherche(tableau,2)
"""
    
#Taille des tableaux testés:
X = [50,100,200,400,800,1600]
Y = []
    
for t in X:
    ### [1] * t retourne un tableau de taille n ne contenant que des 1
    ### temps contient le temps d'exécution moyen em millisecondes du code
    temps =  timeit(stmt=code,setup="tableau = "+str([1]*t))
    Y.append(temps)
       
print(X,Y)
    
plt.plot(X,Y)
plt.ylabel('Temps en microsecondes')
plt.xlabel('Taille du tableau')
#Sauvegarde l'image dans le répertoire du programme
plt.savefig("tempsFonctionTaille.png")
#Affiche l'image
plt.show()
```

Exercice

Cryptographie avec le code de César.

César pour ses messages qu’il voulait garder secret utilisait un code qui consistait à effectuer un décalage dans l’alphabet. Ainsi un décalage de trois remplaçait a par d , b par e , …, z par c .

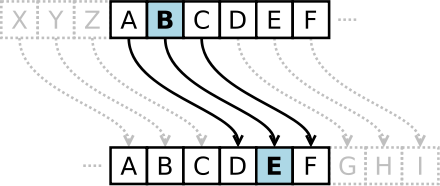
Ce chiffrage est bien trop simple et n’assure aucune sécurité. Au début d’Internet, le ROT13, qui veut dire un décalage de 13 lettres dans l’alphabet, était utilisé pour éviter de spoiler.

Dans le fichier Python de votre programme, recopier l’alphabet:

alphabet = ['a', 'b', 'c', 'd', 'e', 'f', 
            'g', 'h', 'i', 'j', 'k', 'l', 
            'm', 'n', 'o', 'p', 'q', 'r', 
            's', 't', 'u', 'v', 'w', 'x', 'y', 'z']

Écrire une fonction qui prend en entrée un entier qui représente le décalage et renvoie un tableau qui contient l’alphabet décalé de lettres. Ainsi vous devriez obtenir:
```
>>> print(decaler_alphabet(2))
['c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z', 'a', 'b']
```
L’algorithme est le suivant:
```
alpha est une liste vide
Pour i allant de 0 à longueur de alphabet -1:
    affecter à alpha[i] l'élément d'indice i+n du tableau alphabet.
retouner alpha
```
Pour que les indices restent entre 0 et 25 vous devrez utiliser le reste de la division euclidienne. Dans la lettre d’indice 25 est z . Si le décalage est de 2 lettres, $25 + 2 = 27$ et le reste de 27 par 25 est 2. La lettre qui est associée à z est bien la deuxième d’alphabet soit b .
Écrire une fonction qui prend en entrée une chaîne de caractères qui contient le message à coder et un entier qui est le décalage. Cette fonction renvoie une chaîne de caractères qui est le message coder avec le décalage .

On pourra utiliser la méthode . renvoie le premier indice du tableau qui contient la chaîne de caractères .
Faire un petit programme qui demande à l’utilisateur le décalage qui souhaite, puis lui demande le message à coder et enfin affiche le texte codé. Ne pas oublier que le texte à coder ne peut contenir que les caractères du tableau
Faut-il écrire une nouvelle fonction pour décoder le texte? Pourquoi

Pour en savoir plus et source de l’image:

https://fr.wikipedia.org/wiki/Chiffrement_par_d%C3%A9calage